Objetivo: Este artículo detalla cómo medir y analizar la respuesta en frecuencia y la distorsión armónica de un dispositivo de sonido utilizando Python. Usaremos un barrido de frecuencias, capturaremos la señal de audio y realizaremos el análisis de la Transformada Rápida de Fourier (FFT).

main.py

import numpy as np
import pyaudio
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
 
def generate_sweep(start_freq, end_freq, duration, sample_rate=44100):
    t = np.linspace(0, duration, int(sample_rate * duration), False)
    sweep = np.sin(2 * np.pi * np.logspace(np.log10(start_freq), np.log10(end_freq), t.size))
    return t, sweep
 
def play_and_record(sweep, duration, sample_rate=44100, channels=1):
    p = pyaudio.PyAudio()
 
    stream = p.open(format=pyaudio.paFloat32,
                    channels=channels,
                    rate=sample_rate,
                    output=True,
                    input=True,
                    frames_per_buffer=1024)
 
    recorded_frames = []
 
    stream.start_stream()
    stream.write(sweep.astype(np.float32).tobytes())
 
    for _ in range(0, int(sample_rate / 1024 * duration)):
        data = stream.read(1024)
        recorded_frames.append(np.frombuffer(data, dtype=np.float32))
 
    stream.stop_stream()
    stream.close()
    p.terminate()
 
    recorded_signal = np.hstack(recorded_frames)
    return recorded_signal
 
def calculate_fft(signal, sample_rate=44100):
    N = len(signal)
    yf = fft(signal)
    xf = fftfreq(N, 1 / sample_rate)[:N // 2]
    return xf, 2.0 / N * np.abs(yf[:N // 2])
 
def plot_response(xf, yf, test_frequency):
    plt.figure(figsize=(10, 6))
 
    # Convert frequencies to be relative to the test_frequency
    relative_xf = xf / test_frequency
 
    plt.plot(relative_xf, 20 * np.log10(yf))
    plt.title('Frequency Response (Logarithmic Scale)')
    plt.xlabel('Frequency Relative to Test Frequency (log scale)')
    plt.ylabel('Intensity (dB)')
    plt.grid()
    plt.xscale('log')
    plt.xlim(1, relative_xf.max())  # Start at 1 (test frequency) and go to max relative frequency
    plt.ylim(20 * np.log10(yf).min(), 20 * np.log10(yf).max())
    plt.axvline(x=1, color='r', linestyle='--')  # Mark the test frequency
    plt.show()
 
if __name__ == "__main__":
    start_freq = 20
    end_freq = 20000
    duration = 10  # Duration in seconds
    sample_rate = 44100
 
    t, sweep = generate_sweep(start_freq, end_freq, duration, sample_rate)
    recorded_signal = play_and_record(sweep, duration, sample_rate)
    xf, yf = calculate_fft(recorded_signal, sample_rate)
    plot_response(xf, yf, 1000)  # Assuming 1 kHz as test frequency

1. Generación del barrido de frecuencias:

• `generate_sweep` crea un barrido logarítmico de frecuencias de `start_freq` a `end_freq` durante `duration` segundos.

2. Reproducción y grabación:

• `play_and_record` reproduce el barrido de frecuencias y simultáneamente graba la señal de audio del micrófono.
• La señal grabada se almacena en `recorded_frames` y se convierte en un array de `numpy`.

3. Cálculo de la FFT:

• `calculate_fft` calcula la FFT de la señal grabada, devolviendo las frecuencias (`xf`) y la magnitud de la FFT (`yf`).

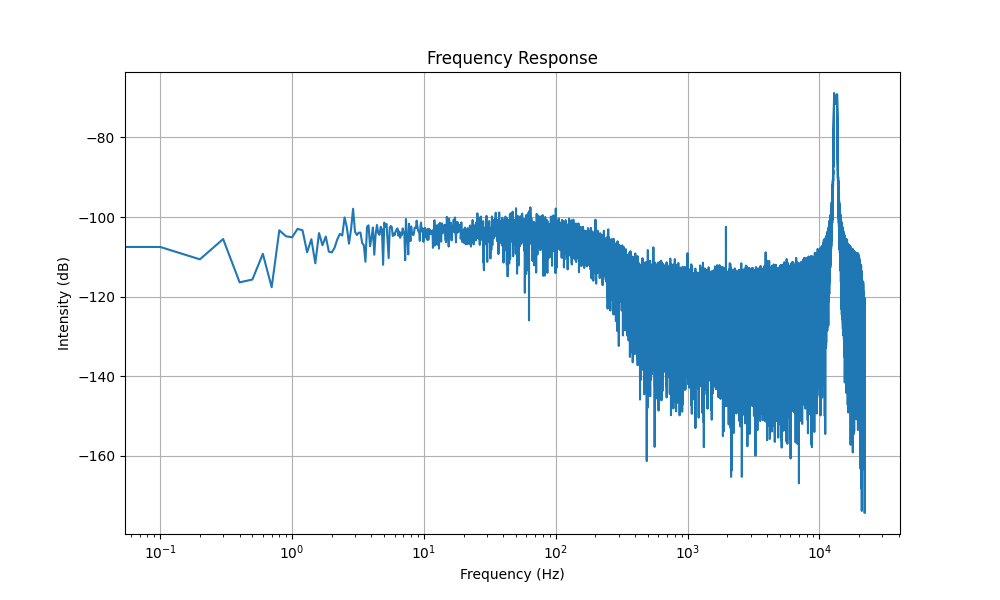
4. Ploteo de la respuesta en frecuencia:

• `plot_response` grafica la magnitud de la FFT en función de la frecuencia, utilizando una escala logarítmica para el eje de las frecuencias.

• Compatibilidad de hardware: Este script asume que el micrófono y los altavoces están bien calibrados y pueden manejar el rango de frecuencias de 20 Hz a 20 kHz. En la práctica, algunos dispositivos de audio pueden no tener una respuesta plana en todo este rango.
• Latencia y sincronización: La latencia de audio y posibles desincronizaciones pueden afectar la precisión del análisis. Este script es una aproximación simple y puede necesitar ajustes para aplicaciones más precisas.
• Seguridad Auditiva: Asegúrate de mantener el volumen a un nivel seguro para evitar daños auditivos, especialmente cuando trabajes con frecuencias altas y barridos de amplio rango.

Prueba este script y ajusta los parámetros según tus necesidades. ¡Buena suerte con tu análisis de la respuesta en frecuencia de tu dispositivo de sonido!