Medición de la Distorsión Armónica Total (THD)

Objetivo: Este script en Python permite inyectar una frecuencia sinusoidal pura de 1 kHz en un sistema de audio y medir la Distorsión Armónica Total (THD) calculando la FFT de la señal capturada.

main.py

import numpy as np
import pyaudio
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
 
def generate_sine_wave(frequency, duration, sample_rate=44100, volume=0.5):
    t = np.linspace(0, duration, int(sample_rate * duration), False)
    tone = volume * np.sin(2 * np.pi * frequency * t)
    return t, tone
 
def play_and_record(tone, duration, sample_rate=44100, channels=1):
    p = pyaudio.PyAudio()
 
    stream = p.open(format=pyaudio.paFloat32,
                    channels=channels,
                    rate=sample_rate,
                    output=True,
                    input=True,
                    frames_per_buffer=1024)
 
    recorded_frames = []
 
    stream.start_stream()
    stream.write(tone.astype(np.float32).tobytes())
 
    for _ in range(0, int(sample_rate / 1024 * duration)):
        data = stream.read(1024)
        recorded_frames.append(np.frombuffer(data, dtype=np.float32))
 
    stream.stop_stream()
    stream.close()
    p.terminate()
 
    recorded_signal = np.hstack(recorded_frames)
    return recorded_signal
 
def calculate_fft(signal, sample_rate=44100):
    N = len(signal)
    yf = fft(signal)
    xf = fftfreq(N, 1 / sample_rate)[:N // 2]
    return xf, 2.0 / N * np.abs(yf[:N // 2])
 
def calculate_thd(xf, yf, fundamental_freq, sample_rate=44100):
    # Find the index of the fundamental frequency
    fundamental_index = np.argmax(np.abs(yf))
    fundamental_power = yf[fundamental_index] ** 2
 
    # Calculate the power of all harmonics
    harmonics_power = np.sum(yf[fundamental_index+1:] ** 2)
 
    # THD is the ratio of the sum of the powers of all harmonics to the power of the fundamental frequency
    thd = np.sqrt(harmonics_power / fundamental_power)
    thd_percentage = thd * 100  # Convert to percentage
 
    return thd_percentage
 
def plot_response(xf, yf):
    plt.figure(figsize=(10, 6))
    plt.plot(xf, 20 * np.log10(yf))
    plt.title('Frequency Response')
    plt.xlabel('Frequency (Hz)')
    plt.ylabel('Intensity (dB)')
    plt.grid()
    plt.xscale('log')
    plt.show()
 
if __name__ == "__main__":
    test_frequency = 1000  # 1 kHz
    duration = 5  # Duration in seconds
    sample_rate = 44100
 
    t, sine_wave = generate_sine_wave(test_frequency, duration, sample_rate)
    recorded_signal = play_and_record(sine_wave, duration, sample_rate)
    xf, yf = calculate_fft(recorded_signal, sample_rate)
    thd = calculate_thd(xf, yf, test_frequency, sample_rate)
 
    print(f"Total Harmonic Distortion (THD): {thd:.2f}%")
    plot_response(xf, yf)

1. Nombre del archivo: `main.py`
2. Dependencias: `numpy`, `pyaudio`, `matplotlib`, `scipy`
3. Funciones:

1. `generate_sine_wave(frequency, duration, sample_rate, volume)`: Genera una onda sinusoidal de la frecuencia y duración especificadas.

2. `play_and_record(tone, duration, sample_rate, channels)`: Reproduce la onda sinusoidal y graba la señal de audio capturada.
3. `calculate_fft(signal, sample_rate)`: Calcula la FFT de la señal grabada.
4. `calculate_thd(xf, yf, fundamental_freq, sample_rate)`: Calcula la Distorsión Armónica Total (THD).
5. `plot_response(xf, yf)`: Grafica la respuesta en frecuencia.

1. Importación de Dependencias:

1. El script importa las bibliotecas necesarias, incluyendo `numpy` para cálculos numéricos, `pyaudio` para manejo de audio, `matplotlib` para graficar, y `scipy` para el cálculo de la FFT.

2. Generación de la Onda Sinusoidal:

1. La función `generate_sine_wave` crea una onda sinusoidal de 1 kHz con la duración especificada.

3. Reproducción y Grabación:

1. La función `play_and_record` reproduce la onda sinusoidal y graba la señal de audio del micrófono, almacenando la señal grabada en un array de `numpy`.

4. Cálculo de la FFT:

1. La función `calculate_fft` calcula la FFT de la señal grabada, devolviendo las frecuencias (`xf`) y la magnitud de la FFT (`yf`).

5. Cálculo de la THD:

1. La función `calculate_thd` calcula la Distorsión Armónica Total (THD) como la relación entre la potencia de todas las componentes armónicas y la potencia de la componente fundamental.

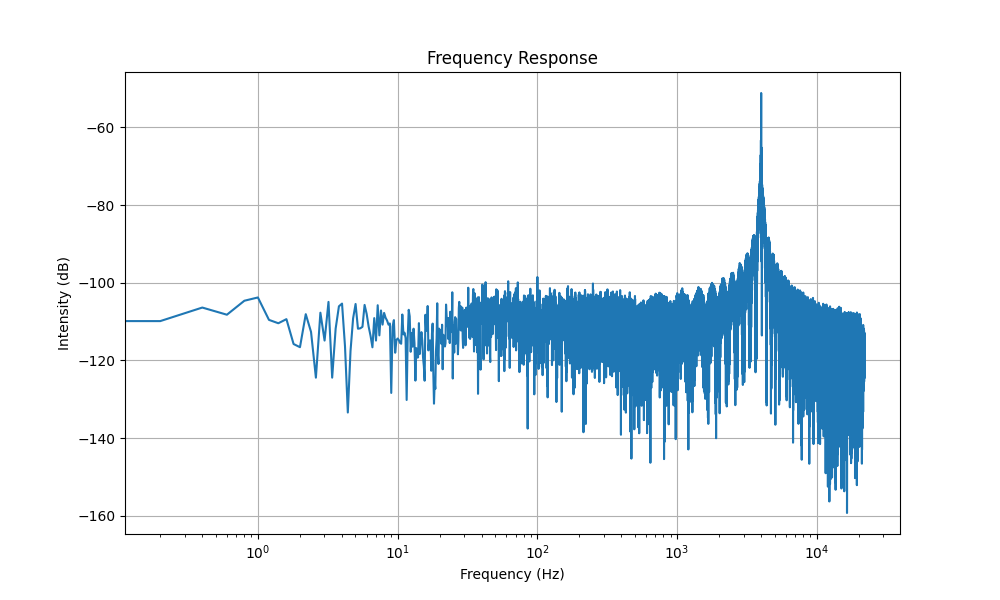
6. Ploteo de la Respuesta en Frecuencia:

1. La función `plot_response` grafica la magnitud de la FFT en función de la frecuencia, utilizando una escala logarítmica para el eje de las frecuencias.

• Para ejecutar el script, corre el archivo `main.py`.
• Asegúrate de que las dependencias necesarias (`numpy`, `pyaudio`, `matplotlib`, `scipy`) estén instaladas.
• Al ejecutarse, el script inyectará una onda sinusoidal de 1 kHz, grabará la señal de entrada, calculará la FFT, y mostrará la Distorsión Armónica Total (THD) así como la respuesta en frecuencia.
• Los resultados se mostrarán en la consola y en una gráfica.

Nota Final: Este script proporciona una forma conveniente de evaluar la calidad de un sistema de audio midiendo la Distorsión Armónica Total (THD) y la respuesta en frecuencia.