Objetivo: Este artículo detalla cómo medir y analizar la respuesta en frecuencia y la distorsión armónica de un dispositivo de sonido utilizando Python. Usaremos un barrido de frecuencias, capturaremos la señal de audio y realizaremos el análisis de la Transformada Rápida de Fourier (FFT).

main.py

import numpy as np
import pyaudio
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
 
def generate_sweep(start_freq, end_freq, duration, sample_rate=44100):
    t = np.linspace(0, duration, int(sample_rate * duration), False)
    sweep = np.sin(2 * np.pi * np.logspace(np.log10(start_freq), np.log10(end_freq), t.size))
    return t, sweep
 
def play_and_record(sweep, duration, sample_rate=44100, channels=1):
    p = pyaudio.PyAudio()
 
    stream = p.open(format=pyaudio.paFloat32,
                    channels=channels,
                    rate=sample_rate,
                    output=True,
                    input=True,
                    frames_per_buffer=1024)
 
    recorded_frames = []
 
    stream.start_stream()
    stream.write(sweep.astype(np.float32).tobytes())
 
    for _ in range(0, int(sample_rate / 1024 * duration)):
        data = stream.read(1024)
        recorded_frames.append(np.frombuffer(data, dtype=np.float32))
 
    stream.stop_stream()
    stream.close()
    p.terminate()
 
    recorded_signal = np.hstack(recorded_frames)
    return recorded_signal
 
def calculate_fft(signal, sample_rate=44100):
    N = len(signal)
    yf = fft(signal)
    xf = fftfreq(N, 1 / sample_rate)[:N // 2]
    return xf, 2.0 / N * np.abs(yf[:N // 2])
 
def plot_response(xf, yf, test_frequency):
    plt.figure(figsize=(10, 6))
 
    # Convert frequencies to be relative to the test_frequency
    relative_xf = xf / test_frequency
 
    plt.plot(relative_xf, 20 * np.log10(yf))
    plt.title('Frequency Response (Logarithmic Scale)')
    plt.xlabel('Frequency Relative to Test Frequency (log scale)')
    plt.ylabel('Intensity (dB)')
    plt.grid()
    plt.xscale('log')
    plt.xlim(1, relative_xf.max())  # Start at 1 (test frequency) and go to max relative frequency
    plt.ylim(20 * np.log10(yf).min(), 20 * np.log10(yf).max())
    plt.axvline(x=1, color='r', linestyle='--')  # Mark the test frequency
    plt.show()
 
if __name__ == "__main__":
    start_freq = 20
    end_freq = 20000
    duration = 10  # Duration in seconds
    sample_rate = 44100
 
    t, sweep = generate_sweep(start_freq, end_freq, duration, sample_rate)
    recorded_signal = play_and_record(sweep, duration, sample_rate)
    xf, yf = calculate_fft(recorded_signal, sample_rate)
    plot_response(xf, yf, 1000)  # Assuming 1 kHz as test frequency

1. Generación del barrido de frecuencias:

• `generate_sweep` crea un barrido logarítmico de frecuencias de `start_freq` a `end_freq` durante `duration` segundos.

2. Reproducción y grabación:

• `play_and_record` reproduce el barrido de frecuencias y simultáneamente graba la señal de audio del micrófono.
• La señal grabada se almacena en `recorded_frames` y se convierte en un array de `numpy`.

3. Cálculo de la FFT:

• `calculate_fft` calcula la FFT de la señal grabada, devolviendo las frecuencias (`xf`) y la magnitud de la FFT (`yf`).

4. Ploteo de la respuesta en frecuencia:

• `plot_response` grafica la magnitud de la FFT en función de la frecuencia, utilizando una escala logarítmica para el eje de las frecuencias.

• Compatibilidad de hardware: Este script asume que el micrófono y los altavoces están bien calibrados y pueden manejar el rango de frecuencias de 20 Hz a 20 kHz. En la práctica, algunos dispositivos de audio pueden no tener una respuesta plana en todo este rango.
• Latencia y sincronización: La latencia de audio y posibles desincronizaciones pueden afectar la precisión del análisis. Este script es una aproximación simple y puede necesitar ajustes para aplicaciones más precisas.
• Seguridad Auditiva: Asegúrate de mantener el volumen a un nivel seguro para evitar daños auditivos, especialmente cuando trabajes con frecuencias altas y barridos de amplio rango.

Prueba este script y ajusta los parámetros según tus necesidades. ¡Buena suerte con tu análisis de la respuesta en frecuencia de tu dispositivo de sonido!

Tomar la FFT de una señal de barrido de frecuencias puede no ser la mejor manera de analizar la respuesta en frecuencia de un sistema.

Opción 1: Tren de Deltas

Un tren de deltas (o una señal de impulsos) es una buena forma de obtener la respuesta al impulso del sistema, y la FFT de esta respuesta te dará directamente la respuesta en frecuencia. Este método es efectivo, pero requiere que el sistema pueda responder a impulsos rápidos, lo que puede no ser ideal para todos los dispositivos de audio.

Opción 2: Barrido de Frecuencias con Análisis de Potencia

El método de barrido de frecuencias con análisis de la potencia de la señal recibida es más directo y puede ser más adecuado para sistemas de audio. Al saber la frecuencia de cada instante de tiempo, puedes medir directamente la respuesta en frecuencia sin necesidad de transformar la señal.

Vamos a implementar la Opción 2: Barrido de Frecuencias con Análisis de Potencia.

Objetivo: Este artículo detalla cómo medir y analizar la respuesta en frecuencia de un dispositivo de sonido utilizando Python. Usaremos un barrido de frecuencias y analizaremos la potencia de la señal recibida para obtener la respuesta en frecuencia.

main.py

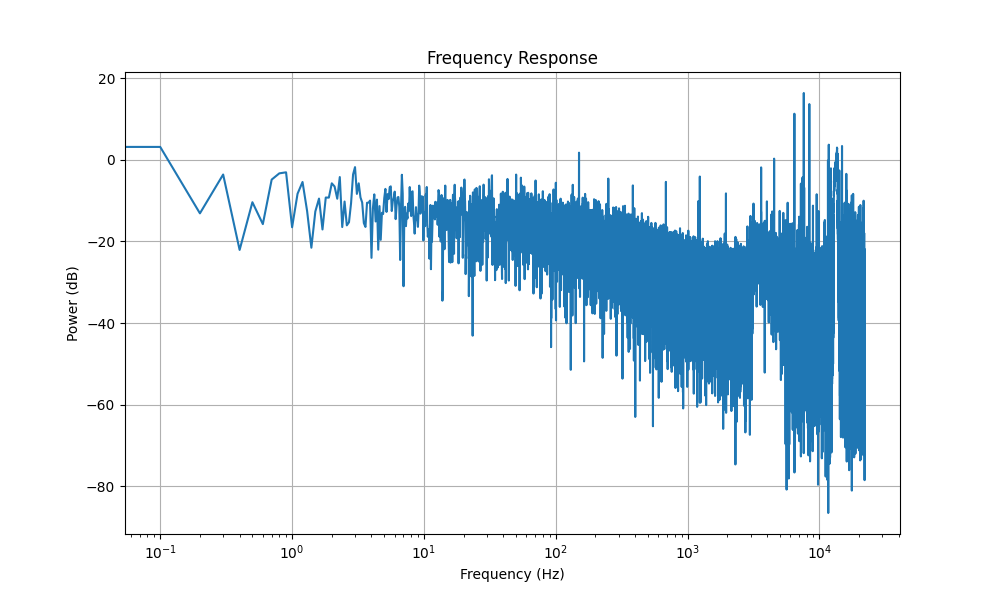
import numpy as np
import pyaudio
import matplotlib.pyplot as plt
 
def generate_sweep(start_freq, end_freq, duration, sample_rate=44100):
    t = np.linspace(0, duration, int(sample_rate * duration), False)
    sweep = np.sin(2 * np.pi * np.logspace(np.log10(start_freq), np.log10(end_freq), t.size))
    return t, sweep
 
def play_and_record(sweep, duration, sample_rate=44100, channels=1):
    p = pyaudio.PyAudio()
 
    stream = p.open(format=pyaudio.paFloat32,
                    channels=channels,
                    rate=sample_rate,
                    output=True,
                    input=True,
                    frames_per_buffer=1024)
 
    recorded_frames = []
 
    stream.start_stream()
    stream.write(sweep.astype(np.float32).tobytes())
 
    for _ in range(0, int(sample_rate / 1024 * duration)):
        data = stream.read(1024)
        recorded_frames.append(np.frombuffer(data, dtype=np.float32))
 
    stream.stop_stream()
    stream.close()
    p.terminate()
 
    recorded_signal = np.hstack(recorded_frames)
    return recorded_signal
 
def analyze_frequency_response(sweep, recorded_signal, sample_rate=44100):
    t = np.linspace(0, len(sweep) / sample_rate, num=len(sweep))
    f = np.logspace(np.log10(20), np.log10(20000), len(sweep))
 
    # Calculate power of the recorded signal
    power = recorded_signal ** 2
 
    return f, power
 
def plot_frequency_response(frequencies, power):
    plt.figure(figsize=(10, 6))
    plt.plot(frequencies, 10 * np.log10(power))
    plt.title('Frequency Response')
    plt.xlabel('Frequency (Hz)')
    plt.ylabel('Power (dB)')
    plt.xscale('log')
    plt.grid()
    plt.show()
 
if __name__ == "__main__":
    start_freq = 20
    end_freq = 20000
    duration = 10  # Duration in seconds
    sample_rate = 44100
 
    t, sweep = generate_sweep(start_freq, end_freq, duration, sample_rate)
    recorded_signal = play_and_record(sweep, duration, sample_rate)
    frequencies, power = analyze_frequency_response(sweep, recorded_signal, sample_rate)
    plot_frequency_response(frequencies, power)

1. Generación del barrido de frecuencias:

1. `generate_sweep` crea un barrido logarítmico de frecuencias de `start_freq` a `end_freq` durante `duration` segundos.

2. Reproducción y grabación:

1. `play_and_record` reproduce el barrido de frecuencias y simultáneamente graba la señal de audio del micrófono.
2. La señal grabada se almacena en `recorded_frames` y se convierte en un array de `numpy`.

3. Análisis de la respuesta en frecuencia:

1. `analyze_frequency_response` calcula la potencia de la señal grabada para cada frecuencia del barrido. Este método asume que la frecuencia cambia logarítmicamente con el tiempo durante el barrido.

4. Ploteo de la respuesta en frecuencia:

1. `plot_frequency_response` grafica la potencia en función de la frecuencia, utilizando una escala logarítmica para el eje de las frecuencias.

• Compatibilidad de hardware: Este script asume que el micrófono y los altavoces están bien calibrados y pueden manejar el rango de frecuencias de 20 Hz a 20 kHz. En la práctica, algunos dispositivos de audio pueden no tener una respuesta plana en todo este rango.

• Latencia y sincronización: La latencia de audio y posibles desincronizaciones pueden afectar la precisión del análisis. Este script es una aproximación simple y puede necesitar ajustes para aplicaciones más precisas.

• Seguridad Auditiva: Asegúrate de mantener el volumen a un nivel seguro para evitar daños auditivos, especialmente cuando trabajes con frecuencias altas y barridos de amplio rango.

sweep_Hanning_5x_movingavg.py

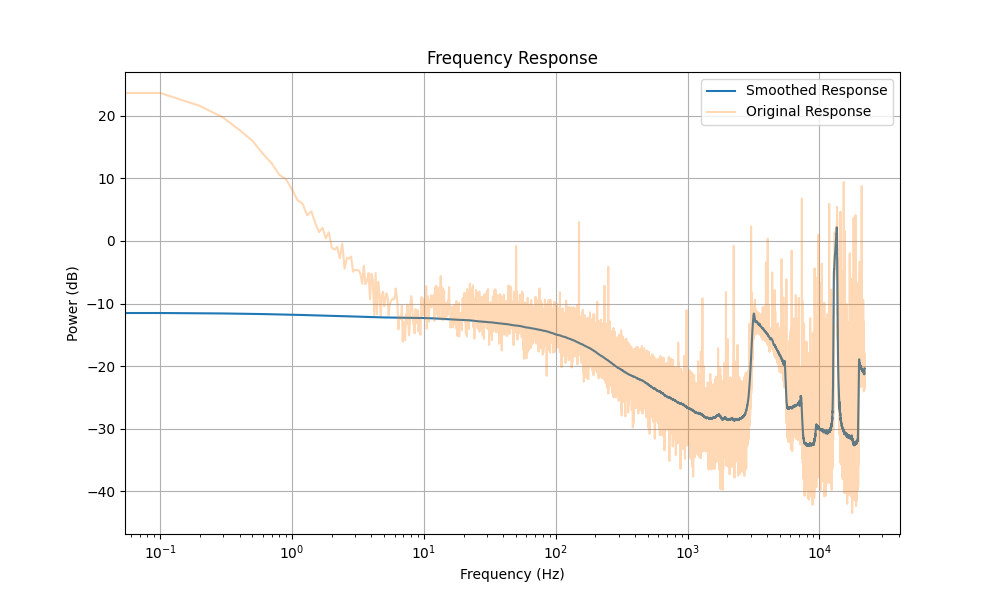
import numpy as np
import pyaudio
import matplotlib.pyplot as plt
from scipy.signal import get_window, butter, filtfilt
from scipy.fft import fft
 
def generate_sweep(start_freq, end_freq, duration, sample_rate=44100):
    t = np.linspace(0, duration, int(sample_rate * duration), False)
    sweep = np.sin(2 * np.pi * np.logspace(np.log10(start_freq), np.log10(end_freq), t.size))
    return t, sweep
 
def play_and_record(sweep, duration, sample_rate=44100, channels=1):
    p = pyaudio.PyAudio()
 
    stream = p.open(format=pyaudio.paFloat32,
                    channels=channels,
                    rate=sample_rate,
                    output=True,
                    input=True,
                    frames_per_buffer=1024)
 
    recorded_frames = []
 
    stream.start_stream()
    stream.write(sweep.astype(np.float32).tobytes())
 
    for _ in range(0, int(sample_rate / 1024 * duration)):
        data = stream.read(1024)
        recorded_frames.append(np.frombuffer(data, dtype=np.float32))
 
    stream.stop_stream()
    stream.close()
    p.terminate()
 
    recorded_signal = np.hstack(recorded_frames)
    return recorded_signal
 
def analyze_frequency_response(sweep, recorded_signal, sample_rate=44100):
    len_min = min(len(sweep), len(recorded_signal))
    sweep = sweep[:len_min]
    recorded_signal = recorded_signal[:len_min]
 
    # Aplicar una ventana de Hann
    window = get_window('hann', len(recorded_signal))
    yf = fft(recorded_signal * window)
    xf = np.fft.fftfreq(len(recorded_signal), 1 / sample_rate)
 
    # Solo tomar la parte positiva del espectro
    pos_freqs = xf[:len(xf) // 2]
    power = np.abs(yf[:len(yf) // 2]) ** 2
 
    return pos_freqs, power
 
def moving_average(data, window_size):
    return np.convolve(data, np.ones(window_size)/window_size, mode='valid')
 
def plot_frequency_response(frequencies, power):
    power += 1e-10  # Agregar un valor pequeño para evitar log10(0)
    smoothed_power = moving_average(10 * np.log10(power), 1000)  # Ajusta el tamaño de la ventana según sea necesario
 
    plt.figure(figsize=(10, 6))
    plt.plot(frequencies[:len(smoothed_power)], smoothed_power, label='Smoothed Response')
    plt.plot(frequencies, 10 * np.log10(power), alpha=0.3, label='Original Response')
    plt.title('Frequency Response')
    plt.xlabel('Frequency (Hz)')
    plt.ylabel('Power (dB)')
    plt.xscale('log')
    plt.grid()
    plt.legend()
    plt.show()
 
if __name__ == "__main__":
    start_freq = 20
    end_freq = 20000
    duration = 10  # Duración en segundos
    sample_rate = 44100
 
    t, sweep = generate_sweep(start_freq, end_freq, duration, sample_rate)
    recorded_signals = [play_and_record(sweep, duration, sample_rate) for _ in range(5)]
 
    # Promediar las respuestas en frecuencia
    power_avg = np.zeros(len(recorded_signals[0]) // 2)
    for recorded_signal in recorded_signals:
        frequencies, power = analyze_frequency_response(sweep, recorded_signal, sample_rate)
        power_avg += power
    power_avg /= len(recorded_signals)
 
    plot_frequency_response(frequencies, power_avg)